Continous time lowpass filter
 ada beberapa jenis filter dengan berbagai respon terhadap perubahan frekuensi. Respon frekuensi dari sebuah filter biasanya direpresentasikan menggunakan bode plot, dimana pada frekuensi cutoff, amplitudo akan turun -3dB dan terus menurun -20dB tiap dekade frekuensi. continous time lowpass filter juga dapat dideskripsikan kedalam transformasi laplace. Sebagai contoh, 1st order lowpass filter dapat dideskripsikan menggunakan notasi laplace berikut.
ada beberapa jenis filter dengan berbagai respon terhadap perubahan frekuensi. Respon frekuensi dari sebuah filter biasanya direpresentasikan menggunakan bode plot, dimana pada frekuensi cutoff, amplitudo akan turun -3dB dan terus menurun -20dB tiap dekade frekuensi. continous time lowpass filter juga dapat dideskripsikan kedalam transformasi laplace. Sebagai contoh, 1st order lowpass filter dapat dideskripsikan menggunakan notasi laplace berikut. 
dimana s adalah variabel transformasi laplace, τ adalah filter time constant dan K merupakan gain filter.
Bagaimana implementasi single pole lowpass filter kedalam bahasa pemprograman?
Untuk dapat melakukan simulasi lowpass filter didalam perangkat lunak dapat dilakukan dengan mengamati karakteristik filter dalam domain waktu dan permodelan diskrit.
Berdasarkan hukum kirchoff, didefinisikan bahwa kapasitansi adalah:
 (
(
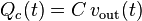 (
(
Dimana 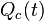 adalah jumlah muatan yang ditampung pada kapasitor dalam waktu t. Jika dilakukan subtitusi persamaan Q menuju persamaan I maka didapat
adalah jumlah muatan yang ditampung pada kapasitor dalam waktu t. Jika dilakukan subtitusi persamaan Q menuju persamaan I maka didapat 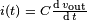 yang dapat disubtitusikan pada persamaan V, sehingga:
yang dapat disubtitusikan pada persamaan V, sehingga:
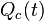 adalah jumlah muatan yang ditampung pada kapasitor dalam waktu t. Jika dilakukan subtitusi persamaan Q menuju persamaan I maka didapat
adalah jumlah muatan yang ditampung pada kapasitor dalam waktu t. Jika dilakukan subtitusi persamaan Q menuju persamaan I maka didapat 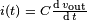 yang dapat disubtitusikan pada persamaan V, sehingga:
yang dapat disubtitusikan pada persamaan V, sehingga:
Persamaan tersebut dapat dideskritkan. untuk lebih sederhana, asumsikan bahwa jumlah sampel input dan output diambil dalam selang waktu  . Katakanlah
. Katakanlah  direpresentasikan dengan rentetan data
direpresentasikan dengan rentetan data 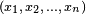 dan
dan  direpresentasikan sebagai sequence data
direpresentasikan sebagai sequence data  , maka dapat dilakukan subtitusi:
, maka dapat dilakukan subtitusi:
 . Katakanlah
. Katakanlah  direpresentasikan dengan rentetan data
direpresentasikan dengan rentetan data 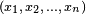 dan
dan  direpresentasikan sebagai sequence data
direpresentasikan sebagai sequence data  , maka dapat dilakukan subtitusi:
, maka dapat dilakukan subtitusi:-

- dengan menata ulang persamaan diatas dapat ditulis sebagai berikut:
implementasi single pole lowpass filter waktu diskret dapat diimplementasikan kedalam persamaan: merupakan smoothing factor dengan nilai
merupakan smoothing factor dengan nilai  . hubungan antara time constant RC,
. hubungan antara time constant RC,  dan smoothing factor
dan smoothing factor  dapat didefinisikan :Jika
dapat didefinisikan :Jika , maka nilai RC akan sama dengan periode sampling. Jika
, maka nilai RC akan sama dengan periode sampling. Jika  , maka
, maka  secara signifikan akan lebih besar dari periode sampling, dan
secara signifikan akan lebih besar dari periode sampling, dan  .Algorithm implementationContoh berikut adalah pseudocode algoritma single pole lowpass filter yang akan mensimulasikan efek dari lowpass filter.
.Algorithm implementationContoh berikut adalah pseudocode algoritma single pole lowpass filter yang akan mensimulasikan efek dari lowpass filter.// Return RC low-pass filter output samples, given input samples, // time interval dt, and time constant RC function lowpass(real[0..n] x, real dt, real RC) var real[0..n] y var real α := dt / (RC + dt) y[0] := x[0] for i from 1 to n y[i] := α * x[i] + (1-α) * y[i-1] return y
Algoritma diatas telah digunakan penulis dalam melakukan smoothing pengambilan data accelerometer dengan α dapat dicari dengan melakukan trial error.
referensi:

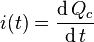

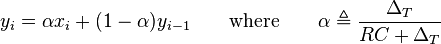
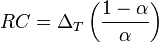



Tidak ada komentar:
Posting Komentar